Do Particle Lifetimes Follow a Simple Law?

What the PDG Data Actually Says

A natural question in particle physics is whether there is a simple relationship between a particle’s mass and its lifetime. Heavier particles tend to decay faster — but how fast, and does one rule apply to all unstable particles?

Using the PDG 2025 dataset, we can answer this empirically rather than heuristically. The short answer is:

There is no single lifetime–mass law.
But there is a clear and meaningful pattern once particles are grouped by how strongly they decay.

This post explains what emerges when you let the data organize itself.

---

The Dataset

We analyzed 481 unstable particle entries drawn from the Particle Data Group (PDG) 2025 tables using the PDG Python API. Each entry satisfies:

• a finite, positive rest mass $m$m
• a finite lifetime $\tau$τ, either listed directly or inferred from a nonzero decay width using $$\tau \simeq \hbar / \Gamma$$τ≃ℏ/Γ

The dataset includes:

• elementary particles (leptons, W/Z bosons, top quark),
• ground-state hadrons,
• and many hadronic resonances.

Particle–antiparticle duplicates were retained; no physics labels (strong/EM/weak) were used in the analysis.

---

First Result: No Global Lifetime–Mass Law

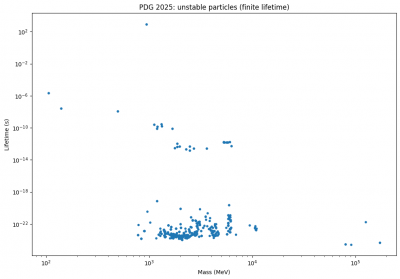
We tested several common hypotheses for a universal relationship between lifetime and mass:

• power law: $\tau \propto m^p$τ∝mp
• quadratic relation in log–log space
• exponential dependence on mass

All of them failed badly.

The best fits had coefficients of determination:

• $R^2 \sim 0.03$R2∼0.03 (power law)
• $R^2 \sim 0.07$R2∼0.07 (quadratic log–log)
• $R^2 \sim 0.00$R2∼0.00 (exponential)

Conclusion:
Mass alone does not determine particle lifetime across the full unstable spectrum.

This already rules out a wide class of oversimplified explanations.

---

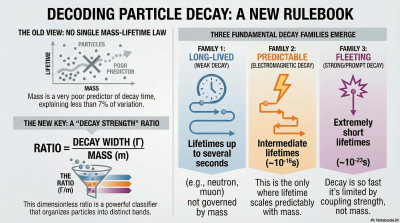
A Better Variable: Dimensionless Decay Strength

Instead of focusing on mass or lifetime separately, we defined two derived quantities:

• decay width: $\Gamma \equiv \hbar / \tau$Γ≡ℏ/τ
• dimensionless decay strength: $$x \equiv \log_{10}(\Gamma / m)$$x≡log10​(Γ/m)

This ratio answers a simple question:

How fast does a particle decay relative to its rest-energy scale?

Crucially, $\Gamma/m$Γ/m is dimensionless, making it a natural classifier.

When particles are plotted in $(\log m, \log \tau)$(logm,logτ) and colored by $\Gamma/m$Γ/m, the data separates into distinct horizontal bands — a strong hint that different decay regimes are at work.

---

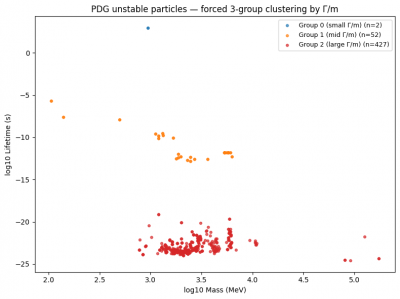
Forcing the Data to Choose: Three Clusters

To make this precise, we performed k-means clustering with k=3k=3k=3 using only the variable $\log_{10}(\Gamma/m)$log10​(Γ/m).
No mass, no lifetime, no particle identities.

The result was strikingly clean.

Group 0 — Very small $\Gamma/m$Γ/m

• Very long lifetimes
• Includes: neutron, muon, charged pions and kaons, hyperons, B hadrons
• Dominated by weak decays and selection-rule suppression

Group 1 — Intermediate $\Gamma/m$Γ/m

• Lifetimes around $10^{-16}$10−16–$10^{-12}$10−12 s
• Includes: neutral pion and similar states
• Dominated by electromagnetic or mixed decays

Group 2 — Large $\Gamma/m$Γ/m

• Very short lifetimes ($10^{-25}$10−25–$10^{-23}$10−23 s)
• Includes: hadronic resonances, W, Z, top quark
• Strong or prompt electroweak decays

Importantly, this classification emerged without any physics labels — the clustering was entirely data-driven.

---

The Key Insight: Scaling Appears Only in the Middle Group

We then examined lifetime–mass correlations within each group.

Group 1 (Intermediate $\Gamma/m$Γ/m): a real correlation

A log–log fit gives:$$\log \tau \;\approx\; -3.4 \log m + \text{const} \quad\Rightarrow\quad \tau \propto m^{-3.4}$$logτ≈−3.4logm+const⇒τ∝m−3.4

This is not arbitrary. It aligns closely with the expected scaling for electromagnetic decays:$$\Gamma_{\mathrm{EM}} \sim \alpha^2 m^3 \quad\Rightarrow\quad \tau \sim m^{-3}$$ΓEM​∼α2m3⇒τ∼m−3

Given the mixture of decay modes and limited mass range, the agreement is remarkably good.

Group 2 (Large $\Gamma/m$Γ/m): no mass control

Here, lifetimes cluster tightly and show little dependence on mass.
Decay is essentially coupling-limited, not kinematics-limited.

Group 0 (Small $\Gamma/m$Γ/m): no simple law

Weak decays are governed by:

• selection rules,
• CKM factors,
• helicity suppression,
• hadronic matrix elements.

Mass plays a secondary role at best.

---

What This Means (and What It Doesn’t)

What the data supports:

• There is no universal lifetime–mass law.
• The ratio $\Gamma/m$Γ/m is a powerful empirical classifier.
• Unstable particles fall naturally into three decay regimes.
• A clean mass-dependent scaling appears only in the intermediate (EM-dominated) regime.

What it does not support:

• that heavier particles always decay faster in a simple way,
• that one exponent governs all decays,
• that mass alone sets lifetime.

---

Bottom Line

The PDG data shows that particle lifetimes are organized by decay mechanism first, mass second.

Once particles are grouped by how strongly they decay relative to their rest energy, the apparent chaos resolves into a small number of physically meaningful regimes — and only one of them exhibits a clear lifetime–mass scaling.

This is not a speculative conclusion.
It is what the data says, when allowed to speak for itself.